Other `bidict` Types#

Now that we’ve covered Basic Usage with the bidict.bidict type, let’s look at some other bidirectional mapping types.

Bidict Types Diagram#

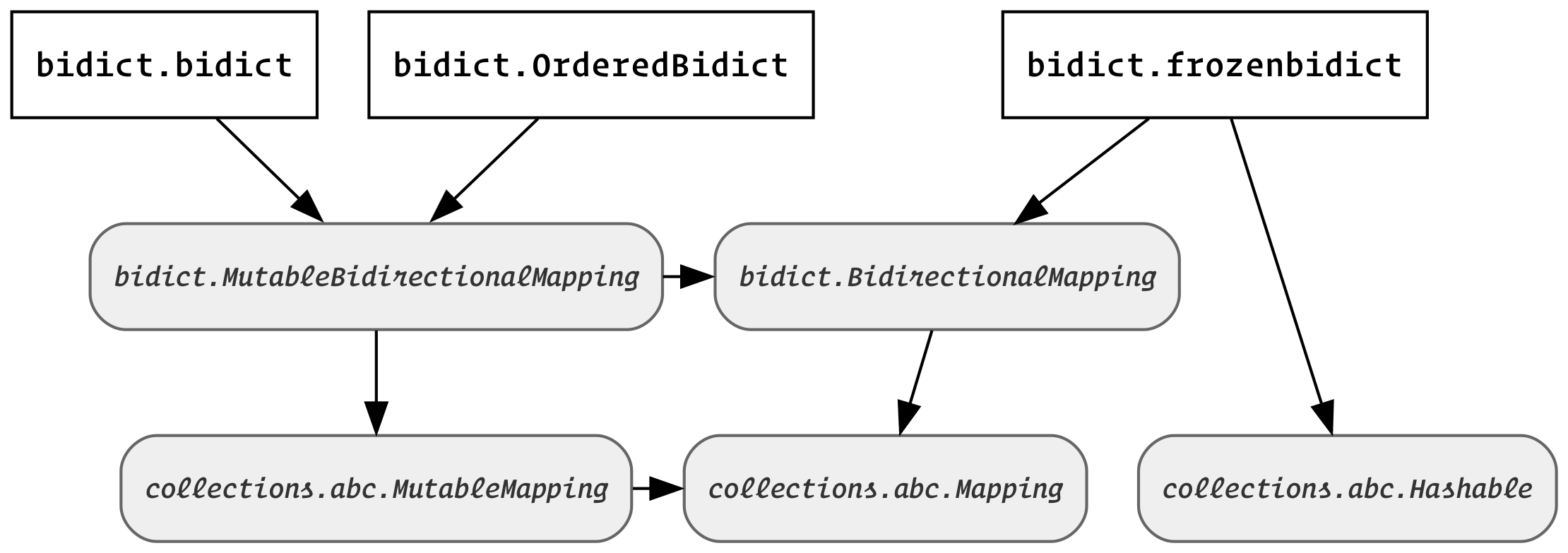
All bidirectional mapping types that bidict provides are subclasses of bidict.BidirectionalMapping. This abstract base class extends collections.abc.Mapping by adding the “inverse” abstractproperty.

As you can see above, bidict.bidict is also a collections.abc.MutableMapping. But bidict provides immutable bidirectional mapping types as well.

`frozenbidict`#

frozenbidict is an immutable, hashable bidirectional mapping type.

As you would expect, attempting to mutate a frozenbidict causes an error:

>>> from bidict import frozenbidict
>>> f = frozenbidict({'H': 'hydrogen'})
>>> f['C'] = 'carbon'
Traceback (most recent call last):
    ...
TypeError: 'frozenbidict' object does not support item assignment

frozenbidict also implements collections.abc.Hashable, so it’s suitable for insertion into sets or other mappings:

>>> my_set = {f}      # not an error
>>> my_dict = {f: 1}  # also not an error

bidict.OrderedBidict is a MutableBidirectionalMapping that preserves the ordering of its items, and offers some additional ordering-related APIs not offered by the unordered bidict types. It’s like a bidirectional version of collections.OrderedDict.

>>> from bidict import OrderedBidict
>>> element_by_symbol = OrderedBidict({
...     'H': 'hydrogen', 'He': 'helium', 'Li': 'lithium'})

>>> element_by_symbol.inverse
OrderedBidict([('hydrogen', 'H'), ('helium', 'He'), ('lithium', 'Li')])

>>> first, second, third = element_by_symbol.values()
>>> first, second, third
('hydrogen', 'helium', 'lithium')

>>> # Insert an additional item and verify it now comes last:
>>> element_by_symbol['Be'] = 'beryllium'
>>> *_, last_item = element_by_symbol.items()
>>> last_item
('Be', 'beryllium')

Additional, efficiently-implemented, order-mutating APIs are provided as well, following the example of OrderedDict.

For example, popitem(last: bool), which makes ordered bidicts suitable for use as FIFO queues, and move_to_end(last: bool), which lets you move any item to either the front or the back of the ordering in constant time.

>>> element_by_symbol.popitem(last=True)   # Remove the last item
('Be', 'beryllium')
>>> element_by_symbol.popitem(last=False)  # Remove the first item
('H', 'hydrogen')

>>> # Re-adding hydrogen after it's been removed moves it to the end:
>>> element_by_symbol['H'] = 'hydrogen'
>>> element_by_symbol
OrderedBidict([('He', 'helium'), ('Li', 'lithium'), ('H', 'hydrogen')])

>>> # But there's also a `move_to_end` method just for this purpose:
>>> element_by_symbol.move_to_end('Li')
>>> element_by_symbol
OrderedBidict([('He', 'helium'), ('H', 'hydrogen'), ('Li', 'lithium')])

>>> element_by_symbol.move_to_end('H', last=False)  # move to front
>>> element_by_symbol
OrderedBidict([('H', 'hydrogen'), ('He', 'helium'), ('Li', 'lithium')])

As with OrderedDict, updating an existing item preserves its position in the order:

>>> element_by_symbol['He'] = 'updated in place!'
>>> element_by_symbol
OrderedBidict([('H', 'hydrogen'), ('He', 'updated in place!'), ('Li', 'lithium')])

Collapsing overwrites#

When setting an item in an ordered bidict whose key duplicates that of an existing item, and whose value duplicates that of a different existing item, the existing item whose value is duplicated will be dropped, and the existing item whose key is duplicated will have its value overwritten in place:

>>> o = OrderedBidict([(1, 2), (3, 4), (5, 6), (7, 8)])
>>> o.forceput(3, 8)  # item with duplicated value (7, 8) is dropped...
>>> o  # and the item with duplicated key (3, 4) is updated in place:
OrderedBidict([(1, 2), (3, 8), (5, 6)])
>>> # (3, 8) took the place of (3, 4), not (7, 8)

>>> o = OrderedBidict([(1, 2), (3, 4), (5, 6), (7, 8)])  # as before
>>> o.forceput(5, 2)  # another example
>>> o
OrderedBidict([(3, 4), (5, 2), (7, 8)])
>>> # (5, 2) took the place of (5, 6), not (1, 2)

`eq()` is order-insensitive#

To ensure that == comparison for any bidict always upholds the transitive property of equality and the Liskov substitution principle, equality tests between a bidict and another mapping are always order-insensitive, even for ordered bidicts:

>>> o1 = OrderedBidict({1: 1, 2: 2})
>>> o2 = OrderedBidict({2: 2, 1: 1})
>>> o1 == o2
True

For order-sensitive equality tests, use equals_order_sensitive():

>>> o1.equals_order_sensitive(o2)
False

(Note that this improves on the behavior of collections.OrderedDict.__eq__(). For more about this, see Python surprises.)

What about order-preserving dicts?#

In CPython 3.6+ and all versions of PyPy, dict preserves insertion order. Since bidicts are built on top of dicts, can we get away with using an unordered bidict in places where you need an order-preserving bidirectional mapping?

(Assume we don’t need the additional APIs offered only by OrderedBidict, such as popitem(last=False).)

Consider this example:

>>> b = bidict({1: -1, 2: -2, 3: -3})
>>> b[2] = 'UPDATED'
>>> b
bidict({1: -1, 2: 'UPDATED', 3: -3})

So far so good, but look what happens here:

>>> b.inverse
bidict({-1: 1, -3: 3, 'UPDATED': 2})

The ordering of items between the bidict and its inverse instance is no longer consistent.

To ensure that ordering is kept consistent between a bidict and its inverse, no matter how it’s mutated, you have to use an ordered bidict:

>>> ob = OrderedBidict({1: -1, 2: -2, 3: -3})
>>> ob[2] = 'UPDATED'
>>> ob
OrderedBidict([(1, -1), (2, 'UPDATED'), (3, -3)])
>>> ob.inverse  # better:
OrderedBidict([(-1, 1), ('UPDATED', 2), (-3, 3)])

An ordered bidict and its inverse always give a consistent ordering of the contained items, even after arbitrary mutations.

If you depend on preserving insertion order, an unordered bidict may be sufficient if:

you’ll never mutate it (in which case, use a frozenbidict), or:
you only mutate by removing and/or adding whole new items, never changing just the key or value of an existing item, or:
you only depend on the order in the forward bidict, and are only changing existing items in the forward direction (i.e. changing values by key, rather than changing keys by value).

That said, if your code depends on the ordering, using an OrderedBidict makes for safer, clearer code.

Of course, the additional order-mutating APIs that OrderedBidict gives you also expand the range of use cases where an OrderedBidict can be used. For example, popitem(last=False) allows using an OrderedBidict as a FIFO queue, as mentioned above.

Reversing a bidict#

All provided bidict types are reversible (since they are backed by dicts, which are themselves reversible on all supported Python versions as of CPython 3.8+).

>>> b = bidict({1: 'one', 2: 'two', 3: 'three'})
>>> list(reversed(b))
[3, 2, 1]
>>> list(reversed(b.items()))  # keys/values/items views are reversible too
[(3, 'three'), (2, 'two'), (1, 'one')]

Polymorphism#

Code that needs to check only whether an object is dict-like should not use isinstance(obj, dict). This check is too specific, because dict-like objects need not actually be instances of dict or a dict subclass. You can see this for many dict-like objects in the standard library:

>>> from collections import ChainMap
>>> chainmap = ChainMap()
>>> isinstance(chainmap, dict)
False

The same is true for all the bidict types:

>>> bi = bidict()
>>> isinstance(bi, dict)
False

A better way to check whether an object is dict-like is to use the Mapping abstract base class (ABC) from the collections.abc module, which provides a number of ABCs intended for this purpose:

>>> isinstance(chainmap, Mapping)
True
>>> isinstance(bi, Mapping)
True

Also note that the proper way to check whether an object is an (im)mutable mapping is to use the MutableMapping ABC:

>>> isinstance(chainmap, MutableMapping)
True
>>> isinstance(bi, MutableMapping)
True

To illustrate this, here’s an example of how you can combine the above with bidict’s own BidirectionalMapping ABC to implement your own check for whether an object is an immutable bidirectional mapping:

>>> def is_immutable_bimap(obj):
...     return (isinstance(obj, BidirectionalMapping)
...             and not isinstance(obj, MutableMapping))

>>> is_immutable_bimap(bidict())
False

>>> is_immutable_bimap(frozenbidict())
True

For more you can do with bidict, check out Extending bidict next.

Other bidict Types#

Bidict Types Diagram#

frozenbidict#

OrderedBidict#